Both myself and @mbaret have been looking into a more robust way we can partition any directed acyclic graph for different compilers/backends. Below is what we came up with:
What’s wrong with the current partitioning algorithm?
-
Lack of support for sub-graphs with multiple outputs.
-
If multiple outputs were supported, the current algorithm wouldn’t be able to resolve data dependency issues, meaning that a graph can be partitioned in such a way that forms 2 (or more) uncomputable sub-graphs. For example the following graph (with each color representing a different compiler) will be partitioned incorrectly.
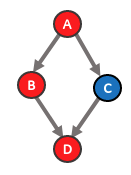
The result will be two sub-graphs: S1[A - B - D)] and S2[C]. However, this cannot be computed since S1 requires the output from S2 and S2 requires an output from S1. The correct way to partition the graph would be S1[A - B], S2[C], S3[D].
Our proposal
An algorithm which resolves these issues.
The principle behind resolving data dependency issues is the property that a data path which leaves a sub-graph cannot re-enter that sub-graph.
- We start by recursively visiting each node in the input graph - starting at the graphs output nodes and only adding a node to a sub-graph once all its parents have sub-graphs assigned.
- Once a node is encountered that can be added we create a set of all the sub-graphs the node is able to join:
- Check whether any of the parent nodes sub-graphs are supported. The is-supported nature of each node will be taken care of by the annotation pass makes (this algorithm also opens up the possibility to annotate inline without a separate annotation pass).
- We maintain a ‘restriction map’ which ensures the principle stated above isn’t violated. Once we have a set of supported sub-graphs we need to take away the sub-graphs that are restricted from one another.
- Following the previous step, we can now add the current node to a sub-graph using one of 2 strategies:
- Join an existing sub-graph (and then check if a merge is possible)
- Create a new sub-graph
- Due to the natural topological ordering of the recursive algorithm, the output is a series of sub-graphs that are correctly partitioned.
The restriction map
The restriction map is an unordered map that keeps track of sub-graphs as they are added and ensures that once a sub-graph has left it (and its parent sub-graphs) are no longer rejoined.
- key - the sub-graph label that uniquely identifies a sub-graph in the graph.
- value - a set containing other sub-graph labels that are restricted from joining the sub-graph represented by the key.
After a new sub-graph is joined or created for a particular node, the restriction map is updated so that the sub-graph just assigned is restricted from rejoining any other parent sub-graphs plus the inherited restrictions from those sub-graphs. Therefore, whenever a path leaves a sub-graph, it remembers it’s not allowed to reenter that sub-graph by adding the sub-graphs it has left as restrictions.
Example
The above much better explained with an example. This particular example shows how the graph can be partitioned correctly involving cases where we: create a new sub-graph, join an existing sub-graph, merge two sub-graphs after joining one and and deal with data dependencies using the restriction map.
Any thoughts are appreciated 

